Higgs Dataset Exercise
Describe the dataset. What type of variable is the target? How many features are being used? How many observations are in the training dataset? How many are used in the validation set?
The goal of building a machine learning model on this dataset is “distinguish between a signal process which produces Higgs bosons and a background process which does not”. The target variable is an integer: either 1 for ‘produced’ or 0 for ‘not produced’. There are 11,000,000 data points, 500,000 of which are used as a test/validation set. Therefore, 10,500,000 points are used in the training set. But to keep it simple, our code uses the first 1,000 points as a testing set, and the next 10,000 points for training.
Additionally, there are 28 features total in this dataset. The first 21 features are regular features used to figure out if there are Higgs boson particles being produced, and the last 7 are functions of the first 21 features.
How did each of the four models perform (tiny, small, medium and large)? Which of the four models performed the best? Which ones performed the worst? Why in your estimation did certain models perform better? Produce a plot that illustrates and compares all four models.
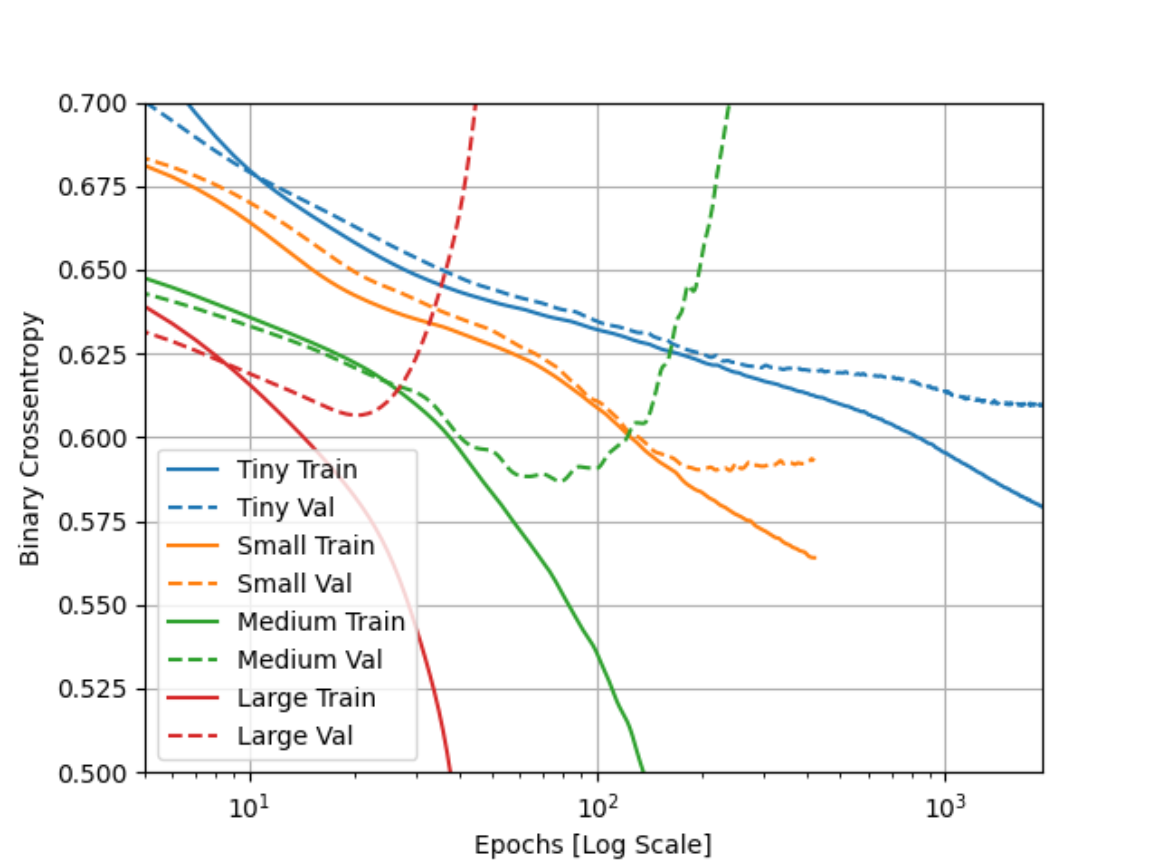
As shown by my plot, I would say that either the Small or Tiny model performed the best. The Small Model has the lowest Binary Crossentropy value for the validation dataset, and it reached that relatively quickly without overfitting. The Tiny model looks like it is the best model for long term testing, as it looks like it somewhat avoided overfitting for all of the epochs displayed and the crossentropy value might get smaller with more testing.
As for which model performed the worst, I would say that it is the Large Model. The validation values suddenly became very large at an early epoch.
The TensorFlow website says that larger models have more power, but if the power is not constrained then the model can easily become overfit and have a higher Binary Crossentropy value. In our case, this is probably what happened, given that with each level, the model increased by 1 layer and (for all except tiny –> small) the nodes in that layer increased by a power of 8.
Apply regularization, then add a drop out layer and finally combine both regularization with a dropout layer. Produce a plot that illustrates and compares all four models. Why in your estimation did certain models perform better?
Here is my graph that compares the 4 methods.
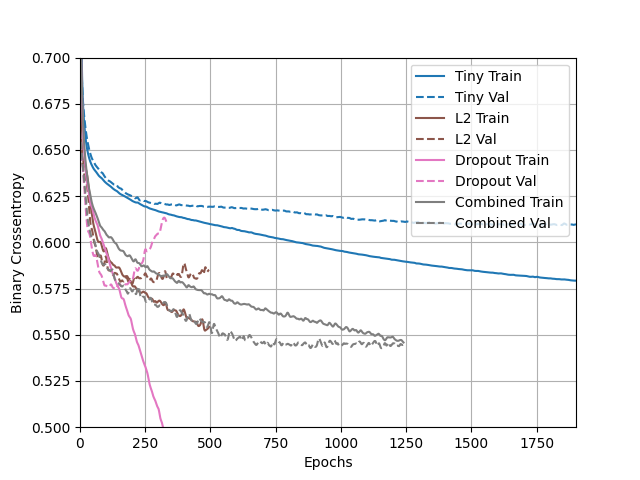
In my opinion, the Tiny model performed better than the other 3 models. It was not too overfit like the Dropout model, and not underfit either. It also was the most consistent over time, and was able to get through many epochs. I just think that this model is the best for the same reason as above. This model is very powerful, and making it very large could result in some wild overfitting like in the Dropout model.
I think that the Dropout model performed poorly because there are so many features, that it may have just set too many features to ‘0’. And then when it ran the testing set, there just weren’t enough features to get accurate outputs. That’s why I think the Combined Model is second place, since it uses both Dropout and L2 regularization, which prevents the weights from going all the way to 0.
What is an overfit model? Why is it important to address it? What are four different ways we have addressed an overfit model thus far?
An overfit model is a model that performs well on the training data, but poorly on the testing data/validation data.
It’s important to address overfitting, because that could mean that the dataset is training itself to only recognize data points from the training set. For example, take a model that was trained to recognize images of flowers. However, the training dataset mostly consisted of yellow flowers while the validation set had pink and yellow flowers. A good model would recognize both pink and yellow flowers, but an overfit model would recognize only yellow flowers.
This could be harmful because an overfit program cannot generalize and make predictions on new data.
The four ways that we have addressed an overfit model are:
- L1 Regularization
- L2 Regularization
- Dropout
- L2 + Dropout